Understanding the 7 1 3 Steane Quantum Error Correction Code
Quantum computing holds immense promise, but its fragility remains a significant hurdle. Quantum bits, or qubits, are incredibly susceptible to errors caused by environmental noise. This is where quantum error correction codes (QECCs) come in – they’re the guardians of quantum information, protecting it from the inevitable mistakes that creep in. Among the various QECC schemes, the 7-1-3 Steane code stands out as a pioneering and widely studied example.
What is the 7-1-3 Steane Code?
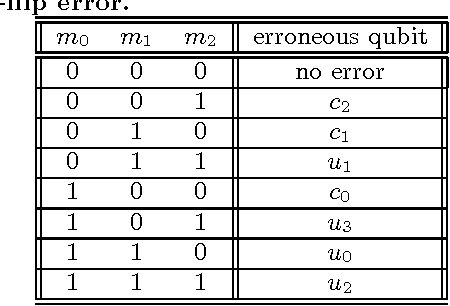
The 7-1-3 Steane code is a quantum error-correcting code that encodes 1 logical qubit into 7 physical qubits. This means it takes the information of a single qubit and distributes it across seven qubits, making it more resilient to errors. The “3” in the name signifies its ability to correct up to 1 error in any of the 7 physical qubits. (quantum error correction, quantum computing, qubit, quantum information)
How Does the Steane Code Work?

The Steane code leverages the power of classical error correction principles adapted for the quantum realm. It uses a clever arrangement of parity checks to detect and correct errors. Think of it like a sophisticated checksum system for quantum information.
Key Features:
Stabilizer Codes: The Steane code belongs to a class of QECCs called stabilizer codes, which use a set of operators (stabilizers) to define the code space and detect errors.
Syndromes: When an error occurs, it causes a change in the stabilizer measurements, generating a syndrome that identifies the type and location of the error.
Correction: Based on the syndrome, the code applies a corrective operation to restore the encoded qubit to its original state.
📌 Note: The Steane code is a block code, meaning it encodes a fixed number of logical qubits (in this case, 1) into a larger block of physical qubits (7).
(stabilizer codes, syndrome, error correction, block code)Why is the Steane Code Important?
The 7-1-3 Steane code holds immense significance in the field of quantum computing for several reasons: * Historical Significance: It was one of the first practical QECCs proposed, paving the way for further developments in the field. * Simplicity and Effectiveness: Its relatively simple structure makes it easier to understand and implement compared to more complex codes. * Benchmarking: It serves as a benchmark for comparing the performance of other QECCs.
Challenges and Future Directions
While the Steane code is a powerful tool, it’s not without its limitations: * Overhead: Encoding a single qubit into 7 physical qubits represents a significant resource overhead. * Error Threshold: Its error correction capability is limited to a single error per block.
Researchers are actively exploring ways to overcome these challenges, such as: * Concatenated Codes: Combining multiple Steane codes to achieve higher error correction thresholds. * Topological Codes: Utilizing the geometry of qubits to achieve more efficient error correction.
What is the difference between classical and quantum error correction?
+Classical error correction deals with bit flips (0 becoming 1 or vice versa), while quantum error correction must also address phase flips and more complex errors due to the superposition and entanglement of qubits.
Can the Steane code correct all types of quantum errors?
+No, the Steane code can correct only single-qubit errors. More advanced codes are needed to handle more complex errors.
What are some real-world applications of quantum error correction?
+Quantum error correction is crucial for building reliable quantum computers capable of solving problems in fields like drug discovery, materials science, and financial modeling.
The 7-1-3 Steane code, while a foundational concept, remains a crucial stepping stone in the journey towards fault-tolerant quantum computing. Its principles continue to inspire the development of more robust and efficient error correction schemes, bringing us closer to unlocking the full potential of quantum information processing. (quantum computing applications, fault-tolerant quantum computing, quantum information processing)



