Understanding Electric Dipoles in 3D Space

Understanding electric dipoles in 3D space is essential for anyone studying electromagnetism or working in fields like physics, chemistry, or electrical engineering. An electric dipole consists of two equal and opposite charges separated by a small distance, creating a fundamental concept in understanding molecular polarity, electric fields, and interactions. This blog explores the intricacies of electric dipoles in three-dimensional space, providing both informative insights and practical applications for readers with varying intents. Whether you're a student, researcher, or professional, this guide will help you grasp the concept and its real-world implications.
What is an Electric Dipole?

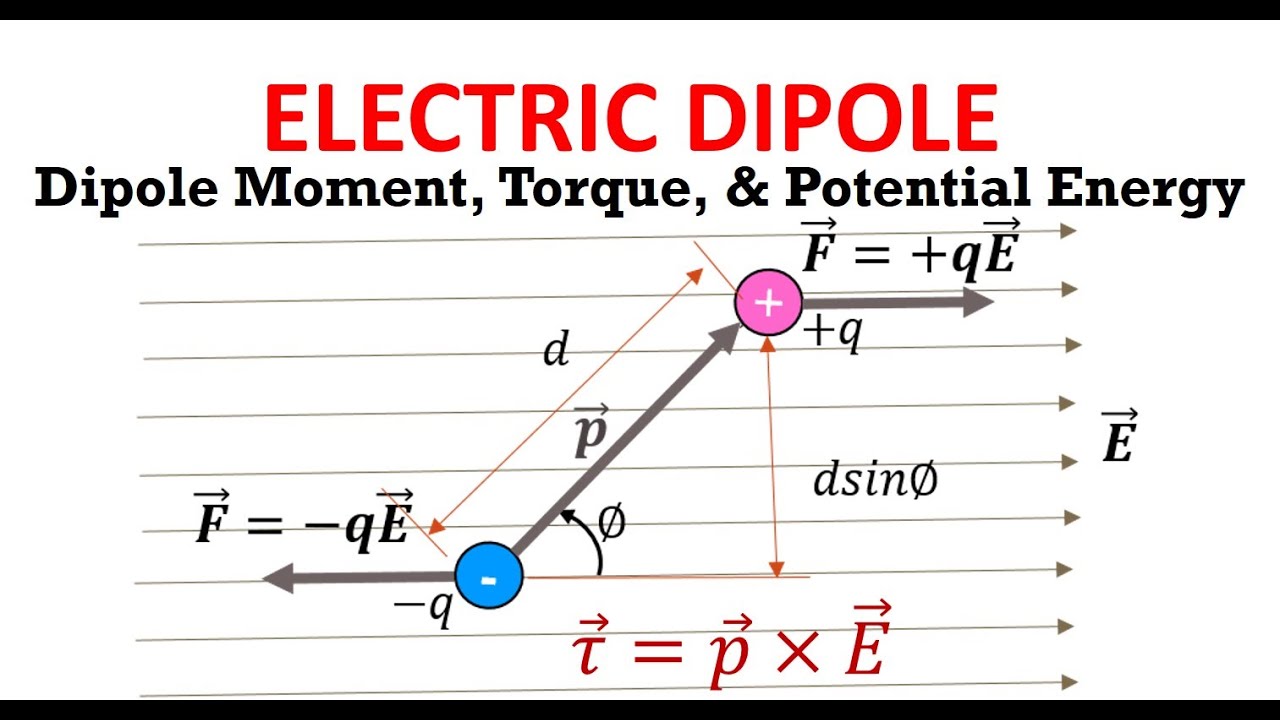
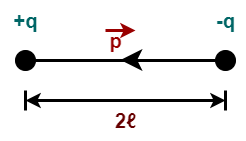
An electric dipole is a pair of equal and opposite charges separated by a distance. In 3D space, it is represented by a vector pointing from the negative charge to the positive charge. The magnitude of this vector is the product of the charge and the separation distance. Electric dipoles are crucial in understanding phenomena like molecular polarity, electric fields, and torque in external fields.
💡 Note: The dipole moment (p) is calculated as p = qd, where q is the charge and d is the separation distance.
Visualizing Electric Dipoles in 3D Space

In three-dimensional space, an electric dipole can be oriented in any direction. This orientation affects its interaction with external electric fields. Visualizing dipoles in 3D helps in understanding concepts like torque, potential energy, and field lines. Tools like vector diagrams and 3D modeling software can aid in this visualization.
| Parameter | Description |
|---|---|
| Dipole Moment (p) | Vector from negative to positive charge |
| Torque (τ) | τ = p × E (cross product of p and electric field E) |
| Potential Energy (U) | U = -p · E (dot product of p and E) |

Applications of Electric Dipoles
Electric dipoles have wide-ranging applications across various fields:
- Chemistry: Understanding molecular polarity and intermolecular forces.
- Physics: Studying electric fields and interactions in materials.
- Engineering: Designing antennas, capacitors, and other electrical components.
- Biology: Analyzing the behavior of biomolecules in electric fields.
Calculating Electric Dipole Fields
The electric field due to a dipole decreases with distance but is stronger along the axial direction compared to the equatorial plane. The formula for the electric field at a point along the axial line is:
E = (2p / 4πε₀r³), where r is the distance from the dipole.
📌 Note: For equatorial points, the formula adjusts to E = (p / 4πε₀r³).
In summary, electric dipoles in 3D space are fundamental to understanding charge distributions and their interactions. By grasping concepts like dipole moments, torque, and field calculations, you can apply this knowledge in chemistry, physics, engineering, and biology. Visualizing dipoles in 3D enhances comprehension, making it easier to tackle complex problems. Whether for academic research or industrial applications, mastering electric dipoles is invaluable.
Checklist for Understanding Electric Dipoles

- Define the dipole moment and its formula.
- Visualize dipole orientation in 3D space.
- Calculate torque and potential energy in an electric field.
- Understand the electric field due to a dipole at axial and equatorial points.
- Explore applications in chemistry, physics, and engineering.
What is the significance of the dipole moment in chemistry?
+The dipole moment helps determine molecular polarity, affecting properties like boiling point, solubility, and intermolecular forces.
How does a dipole interact with an external electric field?
+A dipole experiences torque and aligns itself with the field, leading to changes in potential energy.
What are the units of the dipole moment?
+The dipole moment is measured in Coulomb-meters (C·m) in SI units.
Mastering electric dipoles in 3D space opens doors to advanced concepts in electromagnetism and its applications. Whether you’re exploring molecular interactions, electric fields, or engineering designs, this knowledge is a cornerstone of modern science and technology. Keep exploring, and don’t hesitate to dive deeper into related topics like electromagnetic waves, polarization, and dielectrics to expand your understanding further.



